0. Preface

More resources on website.

??

What is Modern Screw Theory?

What is Modern Differential Geometry?

1. Preview

The ultimate goal of robotics is to create machines that can behave and think like humans.

The robot mechanism is usually constructed by connecting rigid bodies, called links, together by means of joints, so that relative motion between adjacent links becomes possible. The joints are typically actuated by electric motors (AC or DC motors, stepper motors etc.). The ideal motor should operate at relatively low rotational speeds, and be able to generate large forces and torques. So speed reduction and torque amplification are required. Additionally, the brakes may also be attached to stop the robot quickly or to keep a stationary posture.

Sensors are used to measure displacement, velocity, force, torque, and localization.

2. Configuration Space

Robot’s configuration: a specification of the positions of all points of the robot.

The number of degrees of freedom (dof) of a robot is the smallest number of real-valued coordinates needed to represent its configuration.

The n-dimensional space containing all possible configurations of the robot is called the configuration space (C-space).

2.1 Degrees of Freedom of a Rigid Body

The general rule for determining the number of degrees of freedom of a system:

degrees of freedom = (sum of freedoms of the points) - (number of independent constraints)

For robots consist of rigid bodies, the degrees of freedom:

degrees of freedom = (sum of freedoms of the bodies) - (number of independent constraints)

2.2 Degrees of Freedom of a Robot

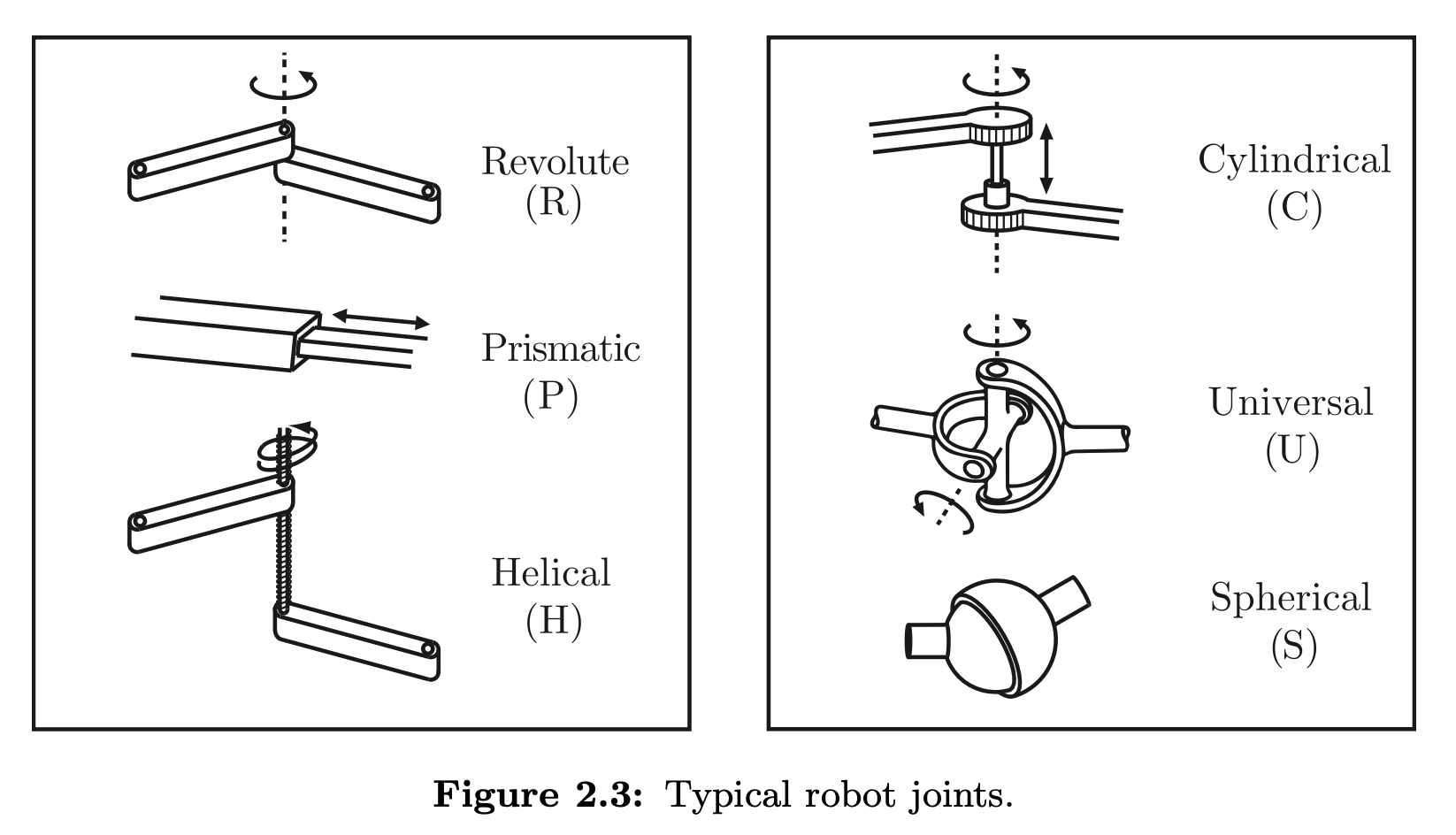
Typical robot joints

The Grubler’s formula for the number of degrees of freedom of the robot is:

dof = m(N - 1 - J) + (sum of dof of all joints)

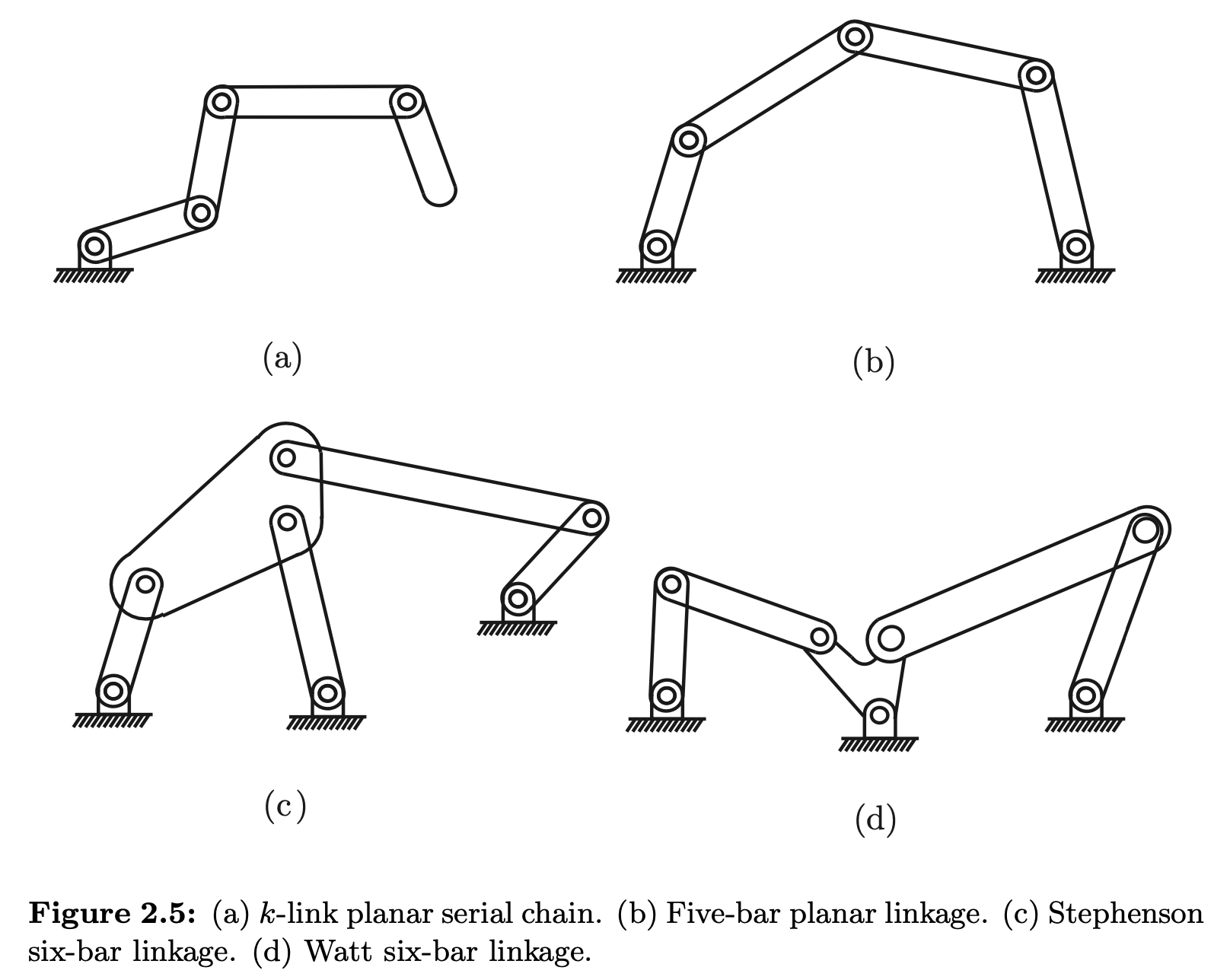
Some classical planar mechanisms

The DoF of Figure 2.5 as following:

  • dof = 3((k + 1) - 1 - k) + k = k
  • dof = 3(5 - 1 - 5) + 5 = 2
  • dof = 3(6 - 1 - 7) + 7 = 1
  • dof = 3(6 - 1 - 7) + 7 = 1

There are exceptions which doesn’t follow the above formula.

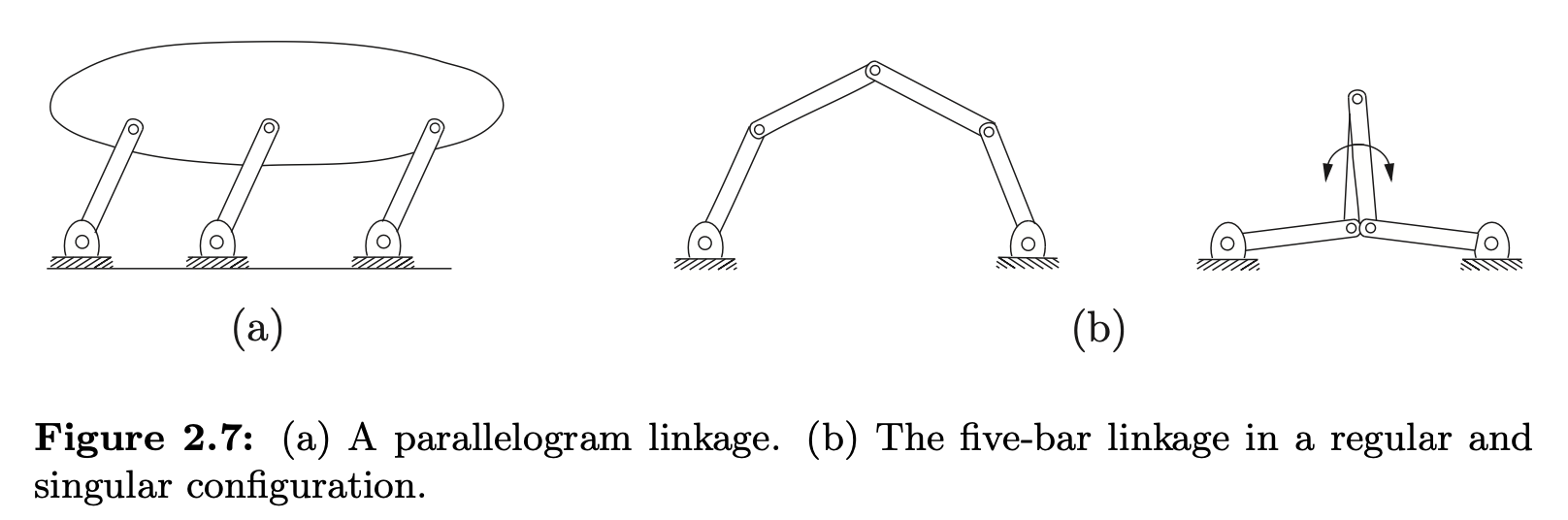
Redundant constraints and singularities

For Figure 2.7(a), the calculation 3(5 - 1 - 6) + 6 = 0 isn’t correct. A mechanism with zero dof is by definition a rigid structure. It’s clear from examining the figure, though, that the mechanism can in fact move with one dof. Indeed, any one of the three parallel links, with its two joints, has no effect on the motion of the mechanism, so we should have calculated dof = 3(4 - 1 - 4) + 4 = 1. In other words, the constraints provided by the joints are not independent, as required by Grubler’s formula.

?

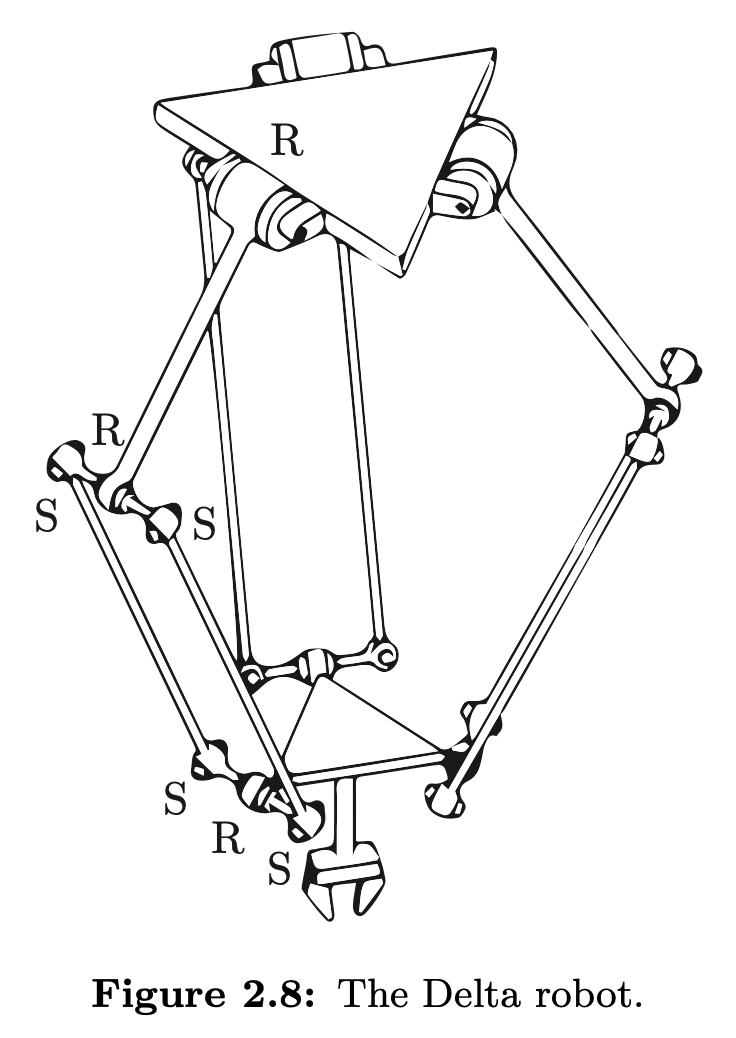
For the Delta robot, the dof of end effector is 3???

The Delta robot

2.3 Configuration Space: Topology and Representation

Topologically Equivalent: if one can be continuously deformed into the other without cutting or gluing.

Note that the topology of a surface is a fundamental property of the space itself and is independent of how we choose coordinates to represent the points in the space.

We need to choose coordinate to represent spaces. A choice of n coordinates, or parameters, to represent an n-dimensional space is called an explicit parametrization of the space.

The singularities of representation is the points where the coordinates change rapidly. If we calculate the velocity as the time rate of change of coordinates. There are two ways to overcome it:

  1. Use more than one coordinate chart on the space, where each coordinate chart is an explicit parametrization covering only a portion of the space such that, within each chart, there is no singularity.
  2. Use an implicit representation instead of an explicit parametrization. An implicit representation views the n-dimensional space as embedded in a Euclidean space of more than n dimensions.

In particular, we use nine numbers, subject to six constraints, to represent the three orientation freedoms of a rigid body in space. This is called a rotation matrix.

2.4 Configuration and Velocity Constraints

Holonomic Constraints: reducing the dimension of the C-space.

Nonholonomic Constraints: reducing the dimension of the feasible velocities of the system but don’t reduce the dimension of the reachable C-space.

2.5 Task Space and Workspace

Task Space: a space in which the robot’s task can be naturally expressed. The decision of how to define the task space is driven by the task, independently of the robot.

Workspace: a specification of the configurations that the end-effector of the robot can reach. The definition of the workspace is primarily driven by robot’s structure, independently of the task.

3. Rigid-Body Motions